Introduction:
In this article, I am going to explain how to find the solutions for the quadratic equation with the Python code. Please install python 3.8 from the link given below to run this code.
https://www.python.org/downloads/
I prefer you to use atom text editor to type your code or to save the given code:
https://atom.io/
You can download the the Quadratic Equation.py from GitHub using the given link:
Code:
#Quadratic equation
a=int(input())
b=int(input())
c=int(input())
d_d = b**2-(4*a*c) #Assigning variables to make the program simpler
d = d_d**(1/2) #Root of b square -4ac
sol1 = ((-b)+d)/(2*a)
sol2 = ((-b)-d)/(2*a)
#Check if solution exists
if d_d < 0:
print('Solution exists in complex numbers')
#Return the solution if it exists in real numbers)
else:
print('x = {0} or x = {1}'.format(sol1,sol2))
Example Input:
1
2
1Output:
x = -1.0 or x = -1.0Code Explanation:
In this code, what we basically do is that, we get the 3 inputs from the user which are the values of a,b and c in a quadratic equation of the form ax2+bx+c.
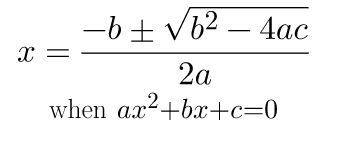
Code (Assignings):
- The variable d_d is assigned the value of b2-4ac.
- The variable d is assigned the value of root of d_d, that is root of b2-4ac.
- Since an equation has 2 values ( ± ).
- The value when used ‘+’ is assigned to the variable sol1.
- Similarly, the value when used ‘-‘ is assigned to the variable sol2.
Code(If…Else):
- In a quadratic equation when the value of b2-4ac is less than 0, then solution is in complex numbers.
- In order to test this, we are checking whether d_d is less than 0 or not.
- If less than 0, the ‘if’ statement is executed where the string (‘Solution exists in complex numbers’) is executed. If not then the real number value is executed (else statement)
Conclusion:
The above article explains the solution to quadratic equation using python coding. If you have any questions or feedback on this, feel free to post in the comments section below.

